Los 7 Problemas Del Milenio, La Respuesta Del US$1 Millón

Introducción

Para el ser humano siempre va a ser apasionante resolver misterios, ya sea planteados por el mismo o por la naturaleza en sí, es por ello que es natural que dentro del mundo de la matemática se desee demostrar todo lo que la conforme, aunque esta demostración no aporte nada a la vida real, por así decirlo, pero es que con esto no se busca darle una utilidad, sino que las demostraciones permiten comprender mejor el problema.

Los problemas abiertos  son los desafíos que  motivan a muchos científicos a lo largo de la historia, con la finalidad de motivar a los matemáticos de este milenio, el Instituto Clay de Matemáticas (CMI) el 24 de mayo del 2000 en el Congreso Internacional de Matemáticos celebrado en París, presentaron siete retos, los cuales si llegan a ser resueltos, tienen una compensación de 1 millón de dólares cada uno, consultar [1].

Ya han pasado 22 años desde que se abrió el reto de los Problemas del Milenio, y hasta la fecha solo se ha resuelto uno oficialmente, la Conjetura de Poincaré, y en septiembre del 2018, el matemático británico Michael Atiyah aseguró haber solucionada la Hipótesis de Riemann, ver [2], pero no convenció a la comunidad matemática.

El único problema de la lista resuelto hasta ahora

Como ya se ha mencionado la Conjetura de Poincaré, es la única que se ha resuelto hasta la fecha, fue establecida en 1904 por el matemático francés Henri Poincaré, y fue el 2002 por el matemático ruso Grigori Perelman, consultar [3].

Grigori Perelman. Imagen tomada de [4].

La conjetura de Poincaré  es un problema topológico, que convierte de forma sencilla  la esfera tridimensional, verificar [5], podemos ver un enunciado más preciso en [6], “Una variedad de dimensión 3 cerradas (compacta y sin borde) con grupo fundamental trivial es homeomorfa a la esfera tridimensional”.

La solución a esta conjetura representa un gran avance en las matemáticas, pero no es el único aporte que ha hecho esta demostración, gracias a la técnica geométrica de teoría del flujo de Hamilton-Perelma, usada en la prueba de la conjetura de Poincaré, Tijana T. Ivancevic, Vladimir G. Ivancevic en [7], propone el uso de un modelo basado en esta teoría para el control de la formación de tumores multicelulares no irrigados (avasculares). Este modelo predictivo puede permitir un mejor control del proceso de proliferación celular en el cáncer, control que podrá ser interferido con medicamentos y, por tanto, con múltiples aplicaciones médicas. En concreto, los autores proponen una terapia basada en anticuerpos monoclonales, así lo resume Villatoro en [8].

Conjetura de Poincaré. Imagen tomada de [9].

Los seis problemas restantes

El problema de P frente a NP

Según el Technology Review en [10], este problema plantea que si dos clases son idénticas, todos los problemas NP son también un problema P. Por lo tanto, si P es Igual a NP, todos los problemas NP contendrán un atajo oculto, lo que permitiría a los ordenadores encontrar rápidamente soluciones perfectas; pero si P no es igual a NP, entonces no existen los atajos mencionados, y la potencia de resolución  de problemas de los cómputos seguirá siendo limitada. Aunque la práctica sugiere que P no es igual NP, pero hasta que no se ofrezca una prueba matemática, la validez de la hipótesis continuará abierta. 

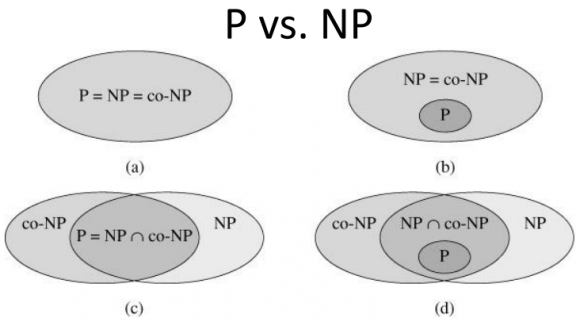
El problema P frente a NP. Imagen tomada de [11]

La conjetura de Hodge

La conjetura de Hodge plantea que las variedades algebraicas proyectivas complejas,  los ciclos de Hodge son una combinación de ciclos algebraicos. Entonces, queda entender que es una variedad algebraica proyectiva, que son los ciclos de Hodge y que son los ciclos algebraicos, la primera es un conjunto de soluciones de un sistema de ecuaciones polinómicas sobre los números complejos; un ciclo algebraico es una subvariedad que se obtiene al añadir a este sistema de ecuaciones nuevas ecuaciones polinómicas; y finalmente, Los ciclos de Hodge son otro tipo de subvariedad que se definen por ciertas propiedades topológicas “agradables”, en lugar de añadiendo nuevas ecuaciones, por lo que son más generales que los ciclos algebraicos. Así lo intentó explicar de una forma simple Villatoro en [12].

La hipótesis de Riemann

En 1859, el matemático alemán Bernhard Riemann publicó un artículo titulado “Sobre el número de primos inferiores a una cantidad dada”, en él presenta la siguiente interrogante “si consideramos un número cualquiera, ¿existe una fórmula que nos diga cuántos números primos menores que él hay?”, o por lo menos así lo relata la página Investigación y ciencia en [13]. En dicho artículo publicado por Riemann, él presenta una función llamada la función Zeta de Riemann, la cuál es la suma de los inversos de todos los enteros positivos elevados un número complejo dado, el demostró que si se si conocieran todos los valores donde esta función se hace cero, se podría obtener una distribución de los números primos, él supone que todos los ceros no triviales de la función zeta, llamados ceros no triviales, se sitúan en la recta formada por los números complejos con parte real igual a 1/2, denominada «recta crítica». Está hipótesis ya ha sido comprobada para billones de ceros de la función zeta, pero aún no se tiene una demostración general que pruebe si la función posee más ceros triviales o no.

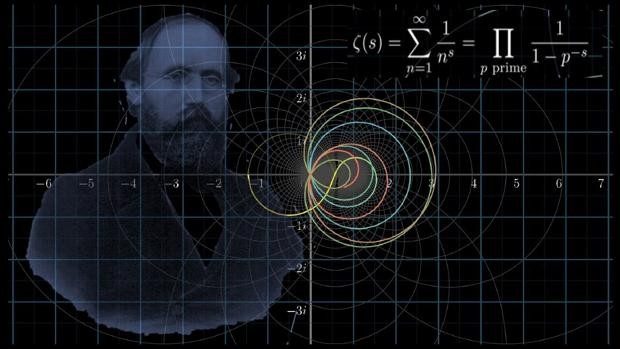
En la ilustración, el matemático alemán Bernhard Riemann junto a la famosa conjetura que lleva su nombre. Imagen tomada de [14].

Este problema es sin duda uno de los más importantes de las matemáticas aún sin resolver, cuya solución presentaría un problema a la seguridad informática, ya que para ello se utilizan los números primos, y al demostrarla se estaría definiendo la estructura de estos, por lo que implicaría buscar otro método.

El algoritmo criptográfico RSA (Rivest, Shamir y Adleman) se utiliza para intercambiar información de forma segura en Internet. Imagen tomada de  [15].

Yang-Mills y el salto de masa ("mass gap")

Yang y Mills introdujeron en 1954 un nuevo concepto que describe las partículas elementales empleando estructuras que también se dan en la geometría, ver [16], la base de esta teoría describe partículas sin masa (gluones). En Ojos [17] nos encontramos con el siguiente enunciado dado por CMI, los experimentos y las simulaciones por computadora sugieren la existencia de una brecha de masa en la solución de la versión cuántica de las ecuaciones de Yang-Pills. Pero no se conoce ninguna prueba de esta propiedad.

Las ecuaciones de Navier-Stokes.

Estas ecuaciones detallan el movimiento de fluidos como líquidos y gases que gobiernan la atmósfera terrestre, las corrientes del océano o el flujo alrededor de vehículos o proyectiles, así lo expresa Ojos en [17], Vázquez presenta un estudio sobre la ecuación de Navier-Stokes, un reto físico-matemático para el siglo XXI [18], de estas ecuaciones se puede observar la siguiente idea, las olas siguen al bote mientras serpentea por el lago, y el aire turbulento de las corrientes que siguen el vuelo en un jet moderno. Matemáticos y físicos creen que una explicación y la predicción de la brisa, y la turbulencia se puede encontrar a través de una comprensión de las soluciones a las ecuaciones de Navier-Stokes. Aunque estas ecuaciones fueron escritas en el siglo XIX, nuestra comprensión de ellos sigue siendo mínima. El desafío es hacer un progreso sustancial hacia una teoría matemática que desbloquee los secretos ocultos en las ecuaciones de Navier-Stokes.

Las ecuaciones de Navier-Stokes se usan para el diseño aerodinámico de los automóviles y los aviones. Imagen tomada de [19].

Conjetura de Birch y Swinnerton-Dyer.

Esta conjetura expone el conjunto de soluciones racionales a las ecuaciones que describen una curva elíptica. Bryan Birch y Peter Swinnerton-Dyer la desarrollaron durante la década de los 60 con la ayuda de la computación mecánica. Hasta la fecha continúa siendo un problema abierto, pero a partir del 2021, se han llegado probar casos especiales de dicha conjetura, ver [20].

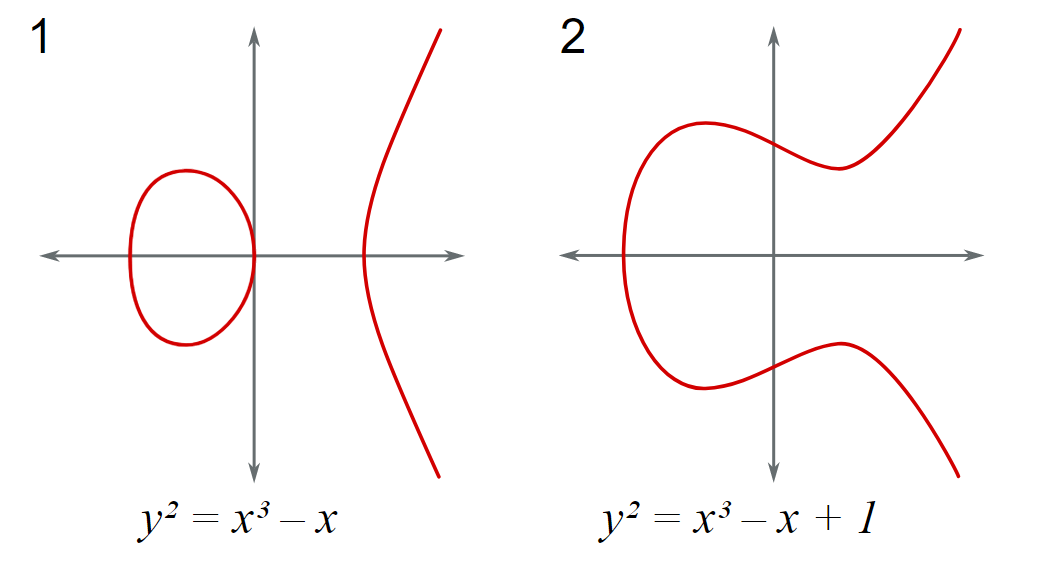
Ejemplo de dos curvas elípticas y su gráfica. Imagen tomada de [21]

Conclusión

El progreso dentro de la ciencia siempre será esencial para la humanidad, y las matemáticas no se quedan atrás, está como rama, juega un papel importante para el avance de sí misma y otras ciencias, que a pesar, de parece una disciplina  que no salé de su mundo abstracto, son sus aplicaciones hasta los menos pensados las que han permitido los diferentes avances en la ciencia y la tecnología, de hecho muchas de sus teorías y campos han surgido dentro de otras ciencias.

Se desea motivar a la comunidad matemática a encontrar la solución de estos problemas con un premio bastante tentador más, sin embargo, cabe resaltar que a la comunidad científica su mayor impulso no siempre lo es el dinero, sino la satisfacción que genera el resolver los enigmas que existen en el mundo y que surgen de nuestra propia invención; es imprescindible mencionar que no son problemas exclusivos a soluciones aportadas por matemáticos, ya que se puede observar que hay problemas que son de las ramas de la computación y la física, y que se espera que su solución posea un formalismo matemático, para que ser evaluado en especial por esta comunidad.

Como se pudo notar, no todos los problemas hoy en día tienen una aplicación directa, pero esto no resta su importancia, pues la utilidad de ellos pueden llegar a surgir una vez que se haya encontrado la solución a estos enigmas, como pasó con las herramientas usadas para la demostración de la conjetura de Poincaré.

Referencia

[1]  Los problemas del milenio. (s. f.). LYCHNOS. Recuperado 21 de abril de 2022, de https://fgcsic.es/lychnos/es_es/articulos/los_problemas_del_milenio

[2] Soriano, A. (2019, 18 enero). ¿Quién era Michael Atiyah? Blogthinkbig.com. https://blogthinkbig.com/atiyah-riemann-matematicas

[3] Imízcoz, M. T. L. (2020, abril 29). La conjetura de Poincaré. Revista Mètode. https://metode.es/revistas-metode/monograficos/la-conjectura-de-poincare.html

[4] Vazquez, A. (2018, 23 julio). Grigori Perelman, el matemático asceta que renunció a un millón de dólares. INVDES. https://invdes.com.mx/ciencia-ms/grigori-perelman-el-matematico-asceta-que-renuncio-a-un-millon-de-dolares/

[5] Imízcoz, M. T. L. (2004). La conjetura de Poincaré. Un problema de topología. Arbor, 178(704), 691-707.

[6] Álvarez, J. G. La Conjetura de Poincaré y Grigori Perelman.

[7] Ivancevic, T. T., & Ivancevic, V. G. (2008). Ricci Flow Model for Avascular Tumor Decay. arXiv preprint arXiv:0806.0691.

[8] Villatoro, F. R. (2020, 5 mayo). ¿Para qué sirve la demostración de la conjetura de poincaré? (o aplicaciones del flujo de ricci al cáncer). La Ciencia de la Mula Francis. https://francis.naukas.com/2008/06/06/para-que-sirve-la-demostracion-de-la-conjetura-de-poincare-o-aplicaciones-del-flujo-de-ricci-al-cancer/#:%7E:text=Este%20modelo%20predictivo%20puede%20permitir,tanto%2C%20con%20m%C3%BAltiples%20aplicaciones%20m%C3%A9dicas.

[9] Imízcoz, M. T. L. (2020, 29 abril). La conjetura de Poincaré. Revista Mètode. https://metode.es/revistas-metode/monograficos/la-conjectura-de-poincare.html

[10] ¿Qué significa «P vs NP» para el resto de nosotros? (2017, 17 agosto). MIT Technology Review. https://www.technologyreview.es//s/1374/que-significa-p-vs-np-para-el-resto-de-nosotros

[11] Dibujo20151211 p vs np with co-np Siddhartha Sen. (2015, 11 diciembre). La Ciencia de la Mula Francis. https://francis.naukas.com/2015/12/11/babai-dice-que-el-isomorfismo-de-grafos-es-un-problema-cuasipolinomico/dibujo20151211-p-vs-np-with-co-np-siddhartha-sen/

[12] Villatoro, F. R. (2019, 8 enero). La conjetura de Hodge explicada para torpes por Dan Freed. La Ciencia de la Mula Francis. https://francis.naukas.com/2011/09/03/la-conjetura-de-hodge-explicada-para-torpes-por-dan-freed/

[13]  La hipótesis de Riemann. (s. f.). Investigación y Ciencia. https://www.investigacionyciencia.es/paginas/la-hiptesis-de-riemann-19763

[14] Nieves, J. M. (2021, 29 noviembre). Proponen una solución a la conjetura de Riemann, uno de los grandes problemas del Milenio. abc. https://www.abc.es/ciencia/abci-sorpresa-solucion-conjetura-riemann-viene-fisica-202111270243_noticia.html?ref=https%3A%2F%2Fwww.google.com%2F

[15] ciencia-para-llevar-csic. (2020, 21 febrero). Números primos: los guardianes de Internet. 20 minutos. https://blogs.20minutos.es/ciencia-para-llevar-csic/2014/06/30/numeros-primos-los-guardianes-de-internet/

[16] Math93, A. (2021, 4 octubre). Los problemas del milenio – P1: Campo de Yang-Mills y el salto de masa. Demostraciones. https://demostracionpy.wordpress.com/2021/10/04/los-problemas-del-milenio-p1-campo-de-yang-mills-y-el-salto-de-masa/

[17]  Ojos, K. (s. f.). Los 7 Problemas Más Grandes De Las Matemáticas. calameo.com. https://es.calameo.com/read/006633237ed31e6a98fe7

[18]  Vázquez, J. L. (2004). La ecuación de Navier-Stokes. Un reto fısico-matemático para el siglo XXI. Departamento de Matemáticas. Univ. Autónoma de Madrid, Real Academia de Ciencias de Zaragoza, 26, 31-56.

[19] Cumulonimbo, O. D. (2020, 9 junio). Las ecuaciones de Navier-Stokes para Dummies. Great Bustard’s Flight. https://greatbustardsflight.blogspot.com/2019/02/las-ecuaciones-de-navier-stokes-para.html

[20] tok.wiki. (s. f.). Conjetura de Birch y Swinnerton-Dyer FondoyHistoria. Hmong. https://hmong.es/wiki/Birch_and_Swinnerton-Dyer_conjecture

[21] Guevara, P. R. (2018, 12 marzo). Un millón de dólares y una plaza en el olimpo de las matemáticas para quien resuelva estos problemas. Xataka. https://www.xataka.com/otros/un-millon-de-dolares-y-una-plaza-en-el-olimpo-de-las-matematicas-para-quien-resuelva-estos-problemas

Bibliografía

BBC News Mundo. (2018, 4 octubre). Los 7 grandes problemas matemáticos cuya resolución se premia con US$1 millón. https://www.bbc.com/mundo/noticias-45706619

Los Problemas del Milenio siguen siendo un misterio. (s. f.). Investigación y Ciencia. https://www.investigacionyciencia.es/noticias/los-problemas-del-milenio-siguen-siendo-un-misterio-19946

Principia Magazine. (2018, 15 marzo). La conjetura de Poincaré - Principia. https://principia.io/2018/03/15/la-conjetura-de-poincare.Ijc0MCI/

Los siete problemas del milenio. (s. f.). MIMOSA. http://mimosa.pntic.mec.es/jgomez53/matema/promilenio.htm

 Muñoz, V. (2004). Cien años de la Conjetura de Poincaré. La Gaceta de la RSME, 7, 629-653.